Szemet gyönyörködtető matek, avagy Fibonacci aránya

2014.01.03 15:03

Előzmény:

Az ember lelkének dallama..Az Ember-dala..Mandala

A Víz üzenete

Fényszív - Szakrális Geometria, az Egy törvénye és a Teremtés

embers-eg.webnode.hu/ujdonsagok/eg-bolt/

 

Fibonacci visszavág, avagy szemet gyönyörködtető matek

 

 

A Fibonacci-számok a matematikában az egyik legismertebb rekurzív sorozat elemei.
Az első két elem 0 és 1, a további elemeket az előző kettő összegeként kapjuk.
Ez a sorozat újból és újból ránk köszön a természetben - egy méh n-generációs őseinek a száma például mindíg az n-ik Fibonacci-szám lesz.
Fibonacci-spirálba rendeződnek a fenyőtoboz és az ananász pikkelyei, a napraforgó magjai, a málna szemei, a karfiol rózsái és egyes kaktuszok tüskéi.

Egy igen elterjedt és közkedvelt eszköz a technikai elemzés eszköztárában a Fibonacci számok alkalmazása, mely azon túl, hogy könnyen és egyszerűen használható, egyértelmű támasz és ellenállási szinteket jelül ki.

 

A Fibonacci számok története igen messzire nyúlik vissza. A XII.-XIII. században élt olasz matematikus, Leonardo Fibonacci nevéhez fűződnek a számok, amint arra a nevéből is lehet következtetni. A matematikai szakkönyvek szerint Fibonacci az egyiptomi piramisok tanulmányozásakor fedezte fel az a számsorozatot, amely azóta is a matematikus nevét viseli. Egyes források szerint azonban Fibonacci ezt a számsorozatot a házinyulak szaporodása során figyelte meg, s tapasztalata szerint egy házinyúl párból egy év alatt 233 pár ivadék származik.

Publikációját Liber Abaci, azaz a Számsorozat Könyve címmel jelentette meg, s benne nem csak elméleti gondolatait vázolta fel, hanem számelméletének számos gyakorlati alkalmazhatóságát is bemutatta. A számsorozat első tőzsde alkalmazásáról azonban nem áll rendelkezésre túl sok információ.

A számsorozat képzése

A szorozat képzése nem túl bonyolult, ám annál érdekesebb. A számok meghatározása úgy történik, hogy az első tagot 1-nek vesszük, majd ezt követően a sorozat következő tagját az azt megelőző két szám összegeként kapjuk. Tehát a sorozat tagjai a következők lesznek:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, stb.

Mindazonáltal a Fibonacci számok több érdekességet mutatnak. Ha ugyanis elosztjuk a számokat a sorozat következő elemével, akkor a hányados egy konstans szám, 0.618 felé konvergál, ha a nagyobbal osztjuk el a kisebbet, akkor pedig a hányados 1.1618 felé konvergál. (A két szám a technikai elemzésben használt Fibonacci szintek tárgyalásakor még visszaköszön.)

Ez a szám ismerős lehet sokak számára, hiszen ezt az arányt már az ókori görögök is ismerték, és aranymetszésnek, korábban pedig "isteni aránynak" hívták. Az aranymetszés arányai megdöbbentő módon a természetben és az emberi alkotásokban számtalan helyen megtalálhatóak (virágok alakjai, az A/4-es papírlap oldalainak aránya, növények levelei, pálmafák ágai, a csigavonal arányai, athéni Parthenón, New York.-i ENSZ Palota, kártyák alakjai, az emberi test köldök feletti és alatti része, egyesek szerint a női mellek elhelyezkedése a felsőtesten, stb.).

Az aranymetszés aránya akkor áll fenn, ha a két szakasz közötti arány pontosan megegyezik az egyenes és a nagyobbik szakasz arányával. A két szakasz arányát a matematikában f-vel jelölik.

 

 

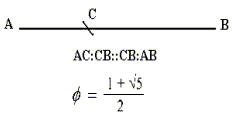
Sokak szerint a Fibonacci számok segítségével sokféle dolgot lehet előre jelezni, különösen a tőzsde területén.

Nem képregény, nem illusztráció, de vizuális stimulátornak elso"rangú.
SPIRÁL-rajongók előnyben... ​